GATE Previous Year Wise Questions
gate 2018
GATE 2019
gate 2016
gate 2016 set 1
GATE 2017 SET 1
GATE 2017 SET2
GATE 2015 SET 1
GATE 2015 SET 2
GATE 2015 SET3
GATE 2014 SET 1
GATE 2014 SET 2
GATE 2013
gate 2009
GATE 2012
gate 2010
GATE 2019
GATE 2014 SET 3
gate 2011
GATE 2008 CS
GATE 2008 IT
GATE 2007 CS
GATE 2007 IT
GATE 2006 CS
GATE 2006 IT
GATE 2005 CS
GATE 2005 IT
GATE 2004 CS
GATE Previous Subject Wise Questions
Data Structures
Algorithms
operating systems
computer organization
Computer Networks
DBMS
Graph Theory
Question 21

Now consider that a value 35 is inserted into this heap. After insertion, the new heap is
A
40, 30, 20, 10, 15, 16, 17, 8, 4, 35
B
40, 35, 20, 10, 30, 16, 17, 8, 4, 15
C
40, 30, 20, 10, 35, 16, 17, 8, 4, 15
D
40, 35, 20, 10, 15, 16, 17, 8, 4, 30
Data Structures
GATE 2015 SET 1
Heap-Tree
Question 22
Consider a complete binary tree where the left and the right subtrees of the root are max-heaps. Thelower bound for the number of operations to convert the tree to a heap is
A
Ω(log n)
B
Ω(n)
C
Ω(n log n)
D
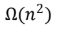
Data Structures
GATE 2015 SET 2
Heap-Tree
Question 23
A binary tree T has 20 leaves. The number of nodes in T having two children is _______.
Submit
Data Structures
GATE 2015 SET 2
Binary-Trees
Question 24

Submit
Data Structures
GATE 2015 SET 2
Question 25
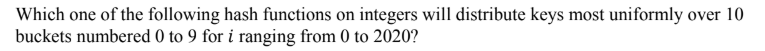
A
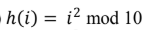
B
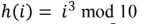
C

D

Data Structures
GATE 2015 SET 2
Hashing
Question 26
Consider a binary tree T that has 200 leaf nodes. Then, the number of nodes in T that have exactlytwo children are ________.
Submit
Data Structures
GATE 2015 SET3
Binary-Trees
Question 27
Given a hash table T with 25 slots that stores 2000 elements, the load factor α for T is____________.
Submit
Data Structures
GATE 2015 SET3
Hashing
Question 28
Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.
A
θ(n)
B
θ(n+m)
C
θ(n2 )
D
θ(m2 )
Data Structures
GATE 2014 SET 1
Graphs
Question 29
Consider a rooted Binary tree represented using pointers. The best upper bound on the time required to determine the number of subtrees having having exactly 4 nodes O(na Logn b). Then the value of a + 10b is ________
A
1
B
2
C
3
D
4
Data Structures
GATE 2014 SET 1
Time-Complexity
Question 30
Consider the directed graph given below.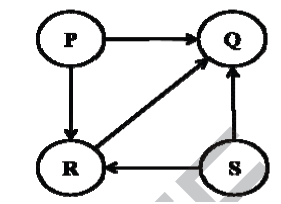
Which one of the following is TRUE?
A
The graph does not have any topological ordering
B
Both PQRS and SRQP are topological orderings
C
Both PSRQ and SPRQ are topological orderings.
D
PSRQ is the only topological ordering.
Data Structures
GATE 2014 SET 1
Graphs
Question 31
Let P be a QuickSort Program to sort numbers in ascending order using the first element as pivot. Let t1 and t2 be the number of comparisons made by P for the inputs {1, 2, 3, 4, 5} and {4, 1, 5, 3, 2} respectively. Which one of the following holds?
A
t1 = 5
B
t1 < t2
C
t1 > t2
D
t1 = t2
Data Structures
GATE 2014 SET 1
Quick-Sort
Question 32
Consider a hash table with 9 slots. The hash function is ?(k) = k mod 9. The collisions are resolved by chaining. The following 9 keys are inserted in the order: 5, 28, 19, 15, 20, 33, 12, 17, 10. The maximum, minimum, and average chain lengths in the hash table, respectively, are
A
3, 0, and 1
B
3, 3, and 3
C
4, 0, and 1
D
3, 0, and 2
Data Structures
GATE 2014 SET 1
Hashing
Question 33
A priority queue is implemented as a Max-Heap. Initially, it has 5 elements. The level-order traversal of the heap is: 10, 8, 5, 3, 2. Two new elements 1 and 7 are inserted into the heap in that order. The level-order traversal of the heap after the insertion of the elements is:
A
10, 8, 7, 3, 2, 1, 5
B
10, 8, 7, 2, 3, 1, 5
C
10, 8, 7, 1, 2, 3, 5
D
10, 8, 7, 5, 3, 2, 1
Data Structures
GATE 2014 SET 2
Heap-Tree
Question 34
Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a data structure for computing.
A
the shortest path between every pair of vertices.
B
the shortest path from W to every vertex in the graph
C
the shortest paths from W to only those nodes that are leaves of T.
D
the longest path in the graph
Data Structures
GATE 2014 SET 2
Graphs
Question 35
The worst case running time to search for an element in a balanced binary search tree with n2n elements is
A
Θ (n log n)
B
Θ (n2n)
C
Θ (n)
D
Θ (log n)
Data Structures
GATE 2012
Binary-Trees
Question 36
The recurrence relation capturing the optimal execution time of the Towers of Hanoi problem with n discs is
A
T(n) = 2T(n - 2) + 2
B
T(n) = 2T(n - 1) + n
C
T(n) = 2T(n/2) + 1
D
T(n) = 2T(n - 1) + 1
Data Structures
Recursion
GATE 2012
Question 37
Suppose a circular queue of capacity (n - 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operations are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are
A
full: (REAR+1)mod n == FRONT
empty: REAR == FRONT
empty: REAR == FRONT
B
full: (REAR+1)mod n == FRONT
empty: (FRONT+1) mod n == REAR
empty: (FRONT+1) mod n == REAR
C
full: REAR == FRONT
empty: (REAR+1) mod n == FRONT
empty: (REAR+1) mod n == FRONT
D
full: (FRONT+1)mod n == REAR
empty: REAR == FRONT
empty: REAR == FRONT
Data Structures
GATE 2012
Queues
Question 38
The height of a tree is defined as the number of edges on the longest path in the tree. The functionshown in the pseudocode below is invoked as height(root) to compute the height of a binary
tree rooted at the tree pointer root
.

The appropriate expressions for the two boxes B1 and B2 are
A
B1: (1+height(n→right))
B2: (1+max(h1,h2))
B2: (1+max(h1,h2))
B
B1: (height(n→right))
B2: (1+max(h1,h2))
B2: (1+max(h1,h2))
C
B1: height(n→right)
B2: max(h1,h2)
B2: max(h1,h2)
D
B1: (1+ height(n→right))
B2: max(h1,h2)
B2: max(h1,h2)
Data Structures
GATE 2012
Binary-Trees
Question 39
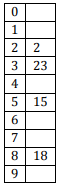
The keys 12, 18, 13, 2, 3, 23, 5 and 15 are inserted into an initially empty hash table of length 10 using open addressing with hash function h(k) = k mod 10 and linear probing. What is the resultant hash table?
A
B
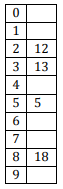
C
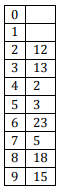
D
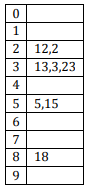
Data Structures
gate 2009
Hashing
Question 40
What is the maximum height of any AVL-tree with 7 nodes? Assume that the height of a tree with a single node is 0.
A
2
B
3
C
4
D
5
Data Structures
gate 2009
AVL-Trees
© 2025 - All rights are reserved- AAIC Technologies pvt ltd

