GATE Previous Year Wise Questions
gate 2018
GATE 2019
gate 2016
gate 2016 set 1
GATE 2017 SET 1
GATE 2017 SET2
GATE 2015 SET 1
GATE 2015 SET 2
GATE 2015 SET3
GATE 2014 SET 1
GATE 2014 SET 2
GATE 2013
gate 2009
GATE 2012
gate 2010
GATE 2019
GATE 2014 SET 3
gate 2011
GATE 2008 CS
GATE 2008 IT
GATE 2007 CS
GATE 2007 IT
GATE 2006 CS
GATE 2006 IT
GATE 2005 CS
GATE 2005 IT
GATE 2004 CS
GATE Previous Subject Wise Questions
Data Structures
Algorithms
operating systems
computer organization
Computer Networks
DBMS
Graph Theory
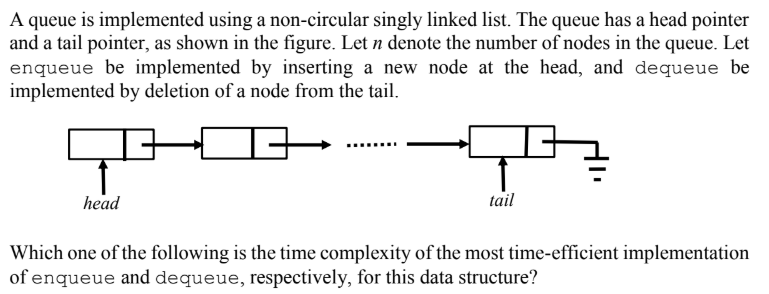
Question 1
Let T be a full binary tree with 8 leaves. (A full binary tree has every level full.) Suppose two leaves a and b of T are chosen uniformly and independently at random. The expected value of the distance between a and b in T (i.e., the number of edges in the unique path between a and b) is (rounded off to 2 decimal places) ___________ .
A
5.71 to 5.73
B
4.85 to 4.86
C
2.71 to 2.73
D
4.24 to 4.26
Data Structures
GATE 2019
Question 2
A
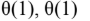
B
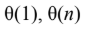
C
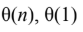
D
Data Structures
gate 2018
Question 3
Submit
Data Structures
gate 2018
Question 4

A
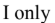
B
C
D
Data Structures
gate 2018
Graphs
Question 5
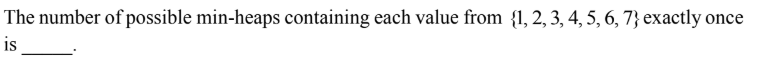
Submit
Data Structures
gate 2018
Heap-Tree
Question 6
A queue is implemented using an array such that ENQUEUE and DEQUEUE operations areperformed efficiently. Which one of the following statements is CORRECT (n refers to the
number of items in the queue)?
A
Both operations can be performed in O(1) time
B
At most one operation can be performed in O(1) time but the worst case time for
the other operation will be Ω(n)
the other operation will be Ω(n)
C
The worst case time complexity for both operations will be Ω(n)
D
Worst case time complexity for both operations will be Ω(logn)
Data Structures
gate 2016 set 1
Question 7
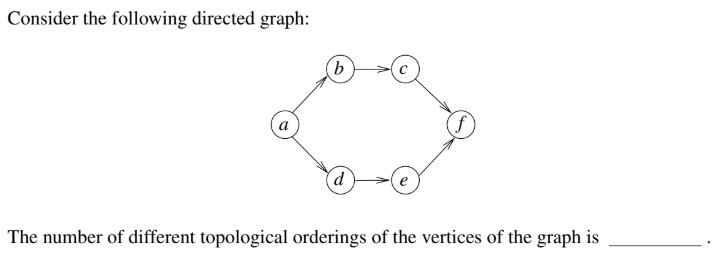
Submit
Data Structures
gate 2016 set 1
Question 8
Let G be a weighted connected undirected graph with distinct positive edge weights. If everyedge weight is increased by the same value, then which of the following statements is/are
TRUE?
P: Minimum spanning tree of G does not change
Q: Shortest path between any pair of vertices does not change
A
P only
B
Q only
C
Neither P nor Q
D
Both P and Q
Data Structures
gate 2016 set 1
Graphs
Question 9
An operator delete(i) for a binary heap data structure is to be designed to delete the item inthe i-th node. Assume that the heap is implemented in an array and i refers to the i-th index
of the array. If the heap tree has depth d (number of edges on the path from the root to the
farthest leaf), then what is the time complexity to re-fix the heap efficiently after the removal
of the element?
A
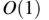
B
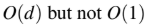
C
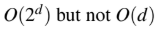
D
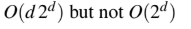
Data Structures
gate 2016 set 1
Question 10

Submit
Data Structures
gate 2016 set 1
Graphs
Question 11

Submit
Data Structures
gate 2016 set 1
Question 12
Breadth First Search (BFS) is started on a binary tree beginning from the root vertex. There isa vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the
maximum possible value of n is _____________
Submit
Data Structures
gate 2016
Question 13

A
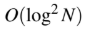
B
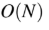
C
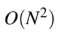
D
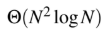
Data Structures
gate 2016
Linked-List
Question 14
The number of ways in which the numbers 1, 2, 3, 4, 5, 6, 7 can be inserted in an empty binarysearch tree, such that the resulting tree has height 6, is __________________
Note: The height of a tree with a single node is 0.
Submit
Data Structures
gate 2016
Question 15

A
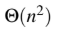
B
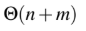
C
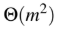
D
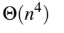
Data Structures
gate 2016
Graphs
Question 16
Let T be a binary search tree with 15 nodes. The minimum and maximum possible heights of T are:Note: The height of a tree with a single node is 0.
A
4 and 15 respectively
B
3 and 14 respectively
C
4 and 14 respectively
D
3 and 15 respectively
Data Structures
GATE 2017 SET 1
Binary-Trees
Question 17
Consider the C code fragment given below.
typedef struct node
{
int data;
node* next ;
} node;
void join(node* m, node* n)
{
node* p = n;
while (p->next != NULL)
{
p = p->next;
}
p–>next = m;
}
Assuming that m and n point to valid NULL- terminated linked lists, invocation of join will
A
append list m to the end of list n for all inputs
B
either cause a null pointer dereference or append list m to the end of list n
C
cause a null pointer dereference for all inputs
D
append list n to the end of list m for all inputs.
Data Structures
GATE 2017 SET 1
Linked-List
Question 18
A Circular queue has been implemented using singly linked list where each node consists of a value and a pointer to next node. We maintain exactly two pointers FRONT and REAR pointing to the front node and rear node of queue. Which of the following statements is/are correct for circular queue so that insertion and deletion operations can be performed in O(1) i.e. constant time.I. Next pointer of front node points to the rear node. II. Next pointer of rear node points to the front node.
A
I only
B
II only
C
Both I and II
D
Neither I nor II
Data Structures
GATE 2017 SET2
Question 19
The height of a tree is the length of the longest root-to-leaf path in it. The maximum and minimumnumber of nodes in a binary tree of height 5 are
A
63 and 6, respectively
B
64 and 5, respectively
C
32 and 6, respectively
D
31 and 5, respectively
Data Structures
GATE 2015 SET 1
Trees
Question 20
Which of the following is/are correct inorder traversal sequence(s) of binary search tree(s)?I. 3, 5, 7, 8, 15, 19, 25
II. 5, 8, 9, 12, 10, 15, 25
III. 2, 7, 10, 8, 14, 16, 20
IV. 4, 6, 7, 9 18, 20, 25
A
I and IV only
B
II and III only
C
II and IV only
D
II only
Data Structures
GATE 2015 SET 1
© 2026 - All rights are reserved- AAIC Technologies pvt ltd

