GATE Previous Year Wise Questions
gate 2018
GATE 2019
gate 2016
gate 2016 set 1
GATE 2017 SET 1
GATE 2017 SET2
GATE 2015 SET 1
GATE 2015 SET 2
GATE 2015 SET3
GATE 2014 SET 1
GATE 2014 SET 2
GATE 2013
gate 2009
GATE 2012
gate 2010
GATE 2019
GATE 2014 SET 3
gate 2011
GATE 2008 CS
GATE 2008 IT
GATE 2007 CS
GATE 2007 IT
GATE 2006 CS
GATE 2006 IT
GATE 2005 CS
GATE 2005 IT
GATE 2004 CS
GATE Previous Subject Wise Questions
Data Structures
Algorithms
operating systems
computer organization
Computer Networks
DBMS
Graph Theory
Question 181
Which of the following statement(s) is / are correct regarding Bellman-Ford shortest path algorithm?P. Always finds a negative weighted cycle, if one
Q. Finds whether any negative weighted cycle is reachable from the source.
A
P Only
B
Q Only
C
Both P and Q
D
Neither P nor Q
Algorithms
gate 2009
Shortest-Path
Question 182
The preorder traversal sequence of a binary search tree is 30, 20, 10, 15, 25, 23, 39, 35, 42. Whichone of the following is the postorder traversal sequence of the same tree?
A
10, 20, 15, 23, 25, 35, 42, 39, 30
B
15, 10, 25, 23, 20, 42, 35, 39, 30
C
15, 20, 10, 23, 25, 42, 35, 39, 30
D
15, 10, 23, 25, 20, 35, 42, 39, 30
Algorithms
GATE 2013
Question 183
Consider the following operation along with Enqueue and Dequeue operations on queues, where k is a global parameter.
MultiDequeue(Q){
m = k
while (Q is not empty and m > 0) {
Dequeue(Q)
m = m - 1
}
}
What is the worst case time complexity of a sequence of n MultiDequeue() operations on an initially empty queue?
A
Θ(n)
B
Θ(n + k)
C
Θ(nk)
D
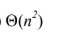
Algorithms
GATE 2013
Time-Complexity
Question 184
The worst case running time to search for an element in a balanced binary search tree with n2n elements is
A
Θ (n log n)
B
Θ (n2n)
C
Θ (n)
D
Θ (log n)
Data Structures
GATE 2012
Binary-Trees
Question 185
The recurrence relation capturing the optimal execution time of the Towers of Hanoi problem with n discs is
A
T(n) = 2T(n - 2) + 2
B
T(n) = 2T(n - 1) + n
C
T(n) = 2T(n/2) + 1
D
T(n) = 2T(n - 1) + 1
Data Structures
Recursion
GATE 2012
Question 186
Let W(n) and A(n) denote respectively, the worst case and average case running time of an algorithm executed on an input of size n. Which of the following is ALWAYS TRUE?
A
A(n) = Ω (W(n))
B
A(n) = Θ (W(n))
C
A(n) = O (W(n))
D
A(n) = o (W(n))
Algorithms
GATE 2012
Time-Complexity
Question 187
Let G be a weighted graph with edge weights greater than one and G' be the graph constructed by squaring the weights of edges in G. Let T and T' be the minimum spanning trees of G and G', respectively, with total weights t and t'. Which of the following statements is TRUE?
A
T' = T with total weight t' = t2
B
T' = T with total weight t'2
C
T' ≠ T but total weight t' = t2
D
None of the above
Algorithms
GATE 2012
Minimum-Spanning-Tree
Question 188
Suppose a circular queue of capacity (n - 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operations are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are
A
full: (REAR+1)mod n == FRONT
empty: REAR == FRONT
empty: REAR == FRONT
B
full: (REAR+1)mod n == FRONT
empty: (FRONT+1) mod n == REAR
empty: (FRONT+1) mod n == REAR
C
full: REAR == FRONT
empty: (REAR+1) mod n == FRONT
empty: (REAR+1) mod n == FRONT
D
full: (FRONT+1)mod n == REAR
empty: REAR == FRONT
empty: REAR == FRONT
Data Structures
GATE 2012
Queues
Question 189
A list of n strings, each of length n, is sorted into lexicographic order using the merge-sort algorithm. The worst case running time of this computation is
A
O (n log n)
B
O (n2 log n)
C
O (n2 + log n)
D
O (n2)
Algorithms
GATE 2012
Merge-Sort
Question 190
Consider the directed graph shown in the figure below. There are multiple shortest paths between vertices S and T. Which one will be reported by Dijstra?s shortest path algorithm? Assume that, in any iteration, the shortest path to a vertex v is updated only when a strictly shorter path to v is discovered.
A
SDT
B
SBDT
C
SACDT
D
SACET
Algorithms
Shortest-Path
GATE 2012
Question 191
Suppose R1(A, B) and R2(C, D) are two relation schemas. Let r1 and r2 be the corresponding relation instances. B is a foreign key that refers to C in R2. If data in r1 and r2 satisfy referential integrity constraints, which of the following is ALWAYS TRUE?
A
∏B (r1) - ∏C (r2) = ∅
B
∏C (r2) - ∏B (r1) = ∅
C
∏B (r1) = ∏C (r2)
D
∏B (r1) - ∏C (r2) ≠ ∅
DBMS
GATE 2012
Question 192
The height of a tree is defined as the number of edges on the longest path in the tree. The functionshown in the pseudocode below is invoked as height(root) to compute the height of a binary
tree rooted at the tree pointer root
.

The appropriate expressions for the two boxes B1 and B2 are
A
B1: (1+height(n→right))
B2: (1+max(h1,h2))
B2: (1+max(h1,h2))
B
B1: (height(n→right))
B2: (1+max(h1,h2))
B2: (1+max(h1,h2))
C
B1: height(n→right)
B2: max(h1,h2)
B2: max(h1,h2)
D
B1: (1+ height(n→right))
B2: max(h1,h2)
B2: max(h1,h2)
Data Structures
GATE 2012
Binary-Trees
Question 193
Consider the above tables A, B and C. How many tuples does the result of the following SQL query contains?
SELECT A.id
FROM A
WHERE A.age > ALL (SELECT B.age
FROM B
WHERE B. name = "arun")
A
4
B
3
C
0
D
1
GATE 2012
Question 194

A
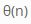
B
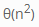
C

D

Algorithms
gate 2009
Time-Complexity
Question 195
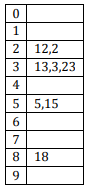
The keys 12, 18, 13, 2, 3, 23, 5 and 15 are inserted into an initially empty hash table of length 10 using open addressing with hash function h(k) = k mod 10 and linear probing. What is the resultant hash table?
A
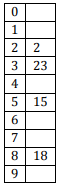
B
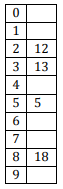
C
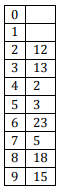
D
Data Structures
gate 2009
Hashing
Question 196
What is the maximum height of any AVL-tree with 7 nodes? Assume that the height of a tree with a single node is 0.
A
2
B
3
C
4
D
5
Data Structures
gate 2009
AVL-Trees
Question 197
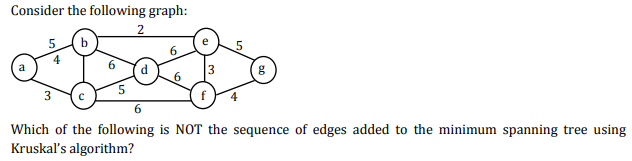
A
(b,e)(e,f)(a,c)(b,c)(f,g)(c,d)
B
(b,e)(e,f)(a,c)(f,g)(b,c)(c,d)
C
(b,e)(a,c)(e,f)(b,c)(f,g)(c,d)
D
(b,e)(e,f)(b,c)(a,c)(f,g)(c,d)
Algorithms
gate 2009
Minimum-Spanning-Tree
Question 198
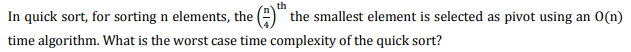
A
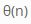
B

C
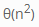
D

Algorithms
gate 2009
Sorting
Question 199
A sub-sequence of a given sequence is just the given sequence with some elements (possibly none or all) left out. We are given two sequences X[m] and Y[n] of lengths m and n respectively, with indexes of X and Y starting from 0. We wish to find the length of the longest common sub-sequence(LCS) of X[m] and Y[n] as l(m,n), where an incomplete recursive definition for the function l(i,j) to compute the length of The LCS of X[m] and Y[n] is given below:
l(i,j) = 0, if either i=0 or j=0
= expr1, if i,j > 0 and X[i-1] = Y[j-1]
= expr2, if i,j > 0 and X[i-1] != Y[j-1]
A
expr1 ≡ l(i-1, j) + 1
B
expr1 ≡ l(i, j-1)
C
expr2 ≡ max(l(i-1, j), l(i, j-1))
D
expr2 ≡ max(l(i-1,j-1),l(i,j))
Algorithms
gate 2009
Dynamic-Programming
Question 200
Consider the data given in the previous question. The values of l(i, j) could be obtained by dynamic programming based on the correct recursive definition of l(i, j) of the form given above, using an array L[M, N], where M = m+1 and N =n+1, such that L[i, j] = l(i, j). Which one of the following statements would be TRUE regarding the dynamic programming solution for the recursive definition of l(i, j)?
A
All elements L should be initialized to 0 for the values of l(i,j) to be properly computed
B
The values of l(i,j) may be computed in a row major order or column major order of L(M,N)
C
The values of l(i,j) cannot be computed in either row major order or column major order of L(M,N)
D
L[p,q] needs to be computed before L[r,s] if either p < r or q < s
Algorithms
gate 2009
Dynamic-Programming
© 2025 - All rights are reserved- AAIC Technologies pvt ltd

